The Critical Path Method (CPM)

The Critical Path Method (CPM) can help you keep your projects on track.

Module 6 of the PM PrepCast is all about Project Schedule Management.

Consider this study program if you're preparing to take your CAPM or PMP Certification exam.

Disclosure: I may receive a commission if you purchase the PM PrepCast with this link.

Critical path schedules will...

Help you identify the activities that must be completed on time in order to complete the whole project on time.
Show you which tasks can be delayed and for how long without impacting the overall project schedule.
Calculate the minimum amount of time it will take to complete the project.
Tell you the earliest and latest dates each activity can start on in order to maintain the schedule.

The Critical Path Method has four key elements...

Critical Path Analysis
Float Determination
Early Start & Early Finish Calculation
Late Start & Late Finish Calculation

Critical Path Analysis

The critical path is the sequence of activities with the longest duration. A delay in any of these activities will result in a delay for the whole project. Below are some critical path examples to help you understand the key elements...

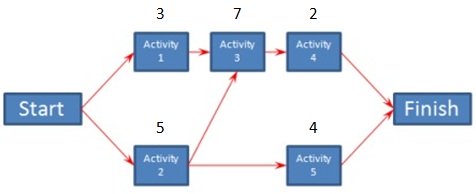Using the Critical Path Method (CPM)

The duration of each activity is listed above each node in the diagram. For each path, add the duration of each node to determine it's total duration. The critical path is the one with the longest duration.

There are three paths through this project...

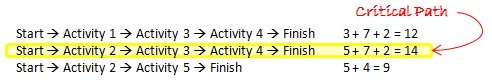Use Critical Path Analysis to find your Critical Path

Float Determination

Once you've identified the critical path for the project, you can determine the float for each activity. Float is the amount of time an activity can slip before it causes your project to be delayed. Float is sometimes referred to as slack.

Figuring out the float using the Critical Path Method is fairly easy. You will start with the activities on the critical path. Each of those activities has a float of zero. If any of those activities slips, the project will be delayed.

Then you take the next longest path. Subtract it's duration from the duration of the critical path. That's the float for each of the activities on that path.

You will continue doing the same for each subsequent longest path until each activities float has been determined. If an activity is on two paths, it's float will be based on the longer path that it belongs to.

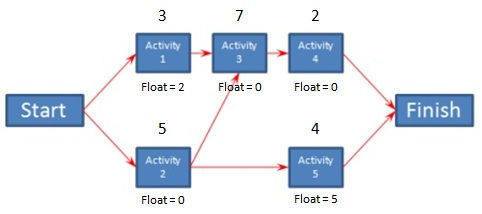Determining Float

Using the critical path diagram from the previous section, Activities 2, 3, and 4 are on the critical path so they have a float of zero.

The next longest path is Activities 1, 3, and 4. Since Activities 3 and 4 are also on the critical path, their float will remain as zero. For any remaining activities, in this case Activity 1, the float will be the duration of the critical path minus the duration of this path. 14 - 12 = 2. So Activity 1 has a float of 2.

The next longest path is Activities 2 and 5. Activity 2 is on the critical path so it will have a float of zero. Activity 5 has a float of 14 - 9, which is 5. So as long as Activity 5 doesn't slip more than 5 days, it won't cause a delay to the project.

Early Start & Early Finish Calculation

The Critical Path Method includes a technique called the Forward Pass which is used to determine the earliest date an activity can start and the earliest date it can finish. These dates are valid as long as all prior activities in that path started on their earliest start date and didn't slip.

Starting with the critical path, the Early Start (ES) of the first activity is one. The Early Finish (EF) of an activity is its ES plus its duration minus one. Using our earlier example, Activity 2 is the first activity on the critical path: ES = 1, EF = 1 + 5 -1 = 5.

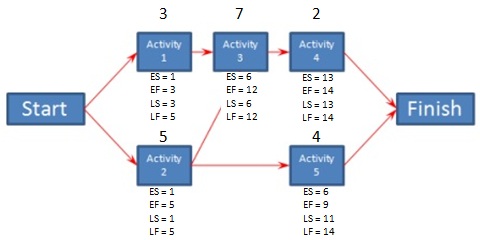Critical Path Schedules

You then move to the next activity in the path, in this case Activity 3. Its ES is the previous activity's EF + 1. Activity 3 ES = 5 + 1 = 6. Its EF is calculated the same as before: EF = 6 + 7 - 1 = 12.

If an activity has more than one predecessor, to calculate its ES you will use the activity with the latest EF.

Late Start & Late Finish Calculation

The Backward Pass is a Critical Path Method techique you can use to determine the latest date an activity can start and the latest date it can finish before it delays the project.

You'll start once again with the critical path, but this time you'l begin from the last activity in the path. The Late Finish (LF) for the last activity in every path is the same as the last activity's EF in the critical path. The Late Start (LS) is the LF - duration + 1.

In our example, Activity 4 is the last activity on the critical path. Its LF is the same as its EF, which is 14. To calculate the LS, subtract its duration from its LF and add one. LS = 14 - 2 + 1 = 13.

You then move on to the next activity in the path. Its LF is determined by subtracting one from the previous activity's LS. In our example, the next Activity in the critical path is Activity 3. Its LF is equal to Activity 4 LS - 1. Activity 3 LF = 13 -1 = 12. It's LS is calculated the same as before by subtracting its duration from the LF and adding one. Activity 3 LS = 12 - 7 + 1 = 6.

You will continue in this manner moving along each path filling in LF and LS for activities that don't have it already filled in.

Pass your PMP Exam!

The PM Exam Simulator is an online exam simulator.

Realistic exam sample questions so you can pass your CAPM or PMP Certification exam.

Disclosure: I may receive a commission if you purchase the PM Exam Simulator with this link.

Manage Your Schedule with the Critical Path Method

The Critical Path Method is an important tool for managing your project's schedule. As you can see, it's not very difficult to determine it's key elements. However, once your project has more than a few activities, critical path scheduling can become tedious.

Luckily, today's project management software provides this information for you. So take a few minutes and learn how to access this information from your software and you'll soon be on top of your schedule and performing critical path analysis like a seasoned pro.

Do You Want More Project Management Tips?

Subscribe to Project Success Tips, my FREE Project Management Newsletter where I share tips and techniques that you can use to get your Project Management Career off to a great start.

As a BONUS for signing up, you'll receive access to my Subscribers Only Download Page! This is where you can download my "Become A Project Manager Checklist" and other project management templates.